A Fluid with a Hole?

– Dwayne Stephens, University of Göttingen

Strong sound waves, such as ultrasound, in a liquid produce bubbles by rupturing the liquid, resulting in an effect called acoustic cavitation1. But to understand this phenomenon more clearly we must first understand the physics behind a single cavitation bubble. To do so we look at a problem posed by W. H. Besant in the early 1900s.

“An infinite mass of homogeneous incompressible fluid acted upon by no forces is at rest, and a spherical portion of the fluid is suddenly annihilated; it is required to find the instantaneous alteration of pressure at any point of the mass, and the time in which the cavity will be filled up, the pressure at an infinite distance being supposed to remain constant.” – Besant

dwayneblog1

Figure 1: A spherical cavity in an infinite, incompressible liquid

Besant wanted to understand what would happen if a spherical portion of an infinite incompressible fluid was suddenly removed. Lord Rayleigh, in his paper of 1917, formulated a theoretical solution to this problem assuming that the spherical cavity was filled with a gas that obeys Boyle’s law2.

The Rayleigh model:

dwayneblog1_eq1

Where R is the bubble radius, ρ is the density, pe is the external pressure in the liquid and pi is the pressure inside the bubble. From the model he found that before complete collapse the pressure near the boundary becomes very great 2. This rapid increase in pressure and consequently temperature during bubble collapse is the reason sonochemistry is possible. More complex models that include gas and vapor inside the bubble, surface tension, liquid viscosity, liquid compressibilty and sound field were later developed, such as the Rayleigh-Plesset model3, Gilmore model4, and Keller-Miksis model5.

These bubble models, which are all based on the Rayleigh model, are nonlinear oscillators. This means that even though oscillations may occur with the same period of the driving wave or sub-harmonically i.e, oscillations repeating after two or more cycles of the driving wave6, the oscillations may also never repeat and be chaotic7. This is interesting because though a simple sinusoidal sound wave drives it, the resulting bubble oscillations may be chaotic7.

Well enough of that. Let’s look at how these curves look under periodic driving by an acoustic wave. Below are two figures, one with steady state oscillation curves and one with chaotic oscillation curves. The points of strong collapses, where the radius diminishes rapidly in an extremely short amount of time, can be seen.

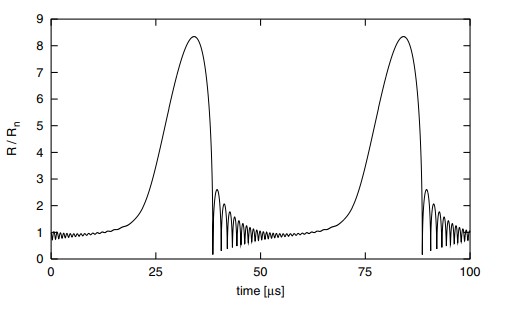
dwayneblog1_pic2

Figure 1: Steady state solution of a 5µm bubble, driving frequency of 20kHz1

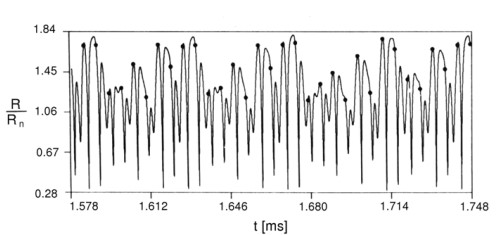
dwayneblog1_pic3

Figure 2: Chaotic solution of a 10µm bubble, driving frequency of 190kHz1

  1. Werner Lauterborn and Thomas Kurz 2010 Rep. Prog. Phys. 73 106501
  2. Lord Rayleigh 1917 On the pressure developed in a liquid during the collapse of a spherical cavity Phil. Mag. Ser. 6 34 94–8
  3. Plesset M S and Prosperetti A 1977 Bubble dynamics and cavitation Annu. Rev. Fluid Mech. 9 145–85
  4. Gilmore F R 1952 The growth or collapse of a spherical bubble in a viscous compressible liquid Report No 26-4
  5. Keller J B and Miksis M 1980 Bubble oscillations of large amplitude J. Acoust. Soc. Am. 68 628–33
  6. Lauterborn W 1976 Investigation of nonlinear oscillations of gas bubbles in liquids J. Acoust. Soc. Am. 59 283–93
  7. Lauterborn W and Parlitz U 1988 Methods of chaos physics and their applications to acoustics J. Acoust. Soc. Am. 84 1975–93